Многофакторный корреляционно - регрессионный анализСтраница 2
2)Связь между x2 и y прямая (так как коэффициент корреляции положительный) и умеренная, так как она находится между 0,41 и 0,50. Поэтому, будем использовать фактор в дальнейших расчётах.
3)Связь между x3 и y прямая (так как коэффициент корреляции положительный) и слабая. Тем не менее, будем использовать фактор в дальнейших расчетах.
Таким образом, два наиболее влиятельных фактора – Индекс потребительских цен – x2 и индекс ВРП - x3. Для имеющихся факторов x2 и x3 составим уравнение множественной регрессии.
Проверим факторы на мультиколлинеарность, для чего рассчитаем коэффициент корреляции rx2x3. Подставив имеющиеся данные (из таблицы 10) в формулу, имеем следующее значение: rx2x3=0,747. Полученный коэффициент говорит об очень высокой связи, поэтому дальнейший анализ по обоим факторам вестись не может. Однако в учебных целях продолжим анализ.
Проводим оценку существенности связи с помощью коэффициента множественной корреляции: R=0,512
Так как R < 0,8, то связь признаем не существенной, но, тем не менее, в учебных целях, проводим дальнейшее исследование.
 |
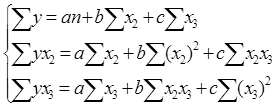Для определения параметров уравнения необходимо решить систему:
Решив систему, получим уравнение: Ŷ=41,57-0,042 x1-0,183x3
Для данного уравнения найдем ошибку аппроксимации:
A=15,12
А> 5%, то данную модель нельзя использовать на практике.
Проведем оценку параметров на типичность. Рассчитаем значения величин:
S2=28,039
ma=0,886; mb=0,0003; mс=0,017;
ta=41,57/0,886=46,919; tb=-0,042/0,0003=-140; tc=-0,183/0,017=-10,77.
Сравним полученные выше значения t для α = 0,05 и числа степеней свободы (n-2) с теоретическим значением t-критерия Стьюдента, который tтеор = 2,1788. Расчетные значения tb и tс < tтеор, значит данные параметры не значимы и данное уравнение не используется для прогнозирования.
Далее оценим существенность совокупного коэффициента множественной корреляции на основе F-критерия Фишера по формуле:
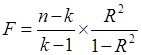
где: n – число уровней ряда; к – число параметров; R – коэффициент множественной корреляции.
После расчета получаем: F=1,41
Сравним Fрасч с Fтеор для числа степеней свободы U1 = 9 и U2 = 2, видим, что 1,41 < 19,40, то есть Fрасч < Fтеор - связь признаётся не существенной, то есть корреляция между факторами x2, x3 и у не существенна.
Другое по теме:
Культура как объект социального познания
В социологии под культурой в широком смысле слова понимают специфическую, генетически ненаследуемую совокупность средств, способов, форм, образцов и ориентиров взаимодействия людей со средой существования, которые они вырабатывают в совме ...
Старшее поколение – фактор экономического развития страны
Как уже отмечалось, главная негативная демографическая тенденция, сложившаяся в России на протяжении последних лет – абсолютное сокращение численности жителей страны. Этот процесс сопровождается радикальными изменениями в возрастной струк ...
Особенности социальной реабилитации инвалидов с нарушением функций
опорно-двигательного аппарата
Проблемы осуществления самообслуживания и самостоятельного передвижения решаются в ходе социально-бытовой реабилитации.
Организация социально-бытовой реабилитации связана с рядом методических подходов, которые лежат в основе технологии э ...